By Matt Worden (Brykovian, Brick)

Alrighty … so what’s this all about? Well, this tutorial is intended to discuss solutions to detecting and determining the results of collisions between game objects that use different collision bounding types. This first part will only cover how to detect whether a collision has occurred. Part 2 will cover how to determine what the physics-based results of the collision should be (with regard to object direction and speed).

So, what do I mean when I use the term "bounding type"? Basically this: When creating the collision detection routines for a game, the programmer needs to determine how they want to go about representing the game objects for those routines. Three bounding types usually come to the forefront:

1. Pixel Perfect – meaning the location of the actual pixels of each sprite are compared to determine if any of them overlap. (This method will not be covered by this tutorial, mainly because there already are a number of good tutorials discussing how to implement this.)

2. Circular – perhaps the easiest of them all, this method imagines a circular boundary around the object. This is usually represented by an OffsetX and OffsetY (to determine the center of the circle, relative to the sprite’s upper-left corner), and a radius. Circle-versus-circle collisions are quick and easy to determine: If the distance between the two circle center points is less than the sum of the two circles’ radii, then you have a collision.

3. Rectangular – a very common approach that imagines a rectangular boundary around the object. This may either match the sprite’s bitmap rectangle, or have adjusted offsets. But, either way, it will result in a common rectangle with top, bottom, left, and right properties. There are a number of tutorials covering how to calculate the intersection of rectangles – even an API function to do the calculations for you! The basics can be summed up by saying: If Object1’s top or bottom is between Object2’s top and bottom, and Object1’s left or ride side is between Object2’s left and right side, then you have a collision.

So, what happens when you have a circular-bounded object that might collide with a rectangular-bounded object? Well, things get a bit more interesting …

First, let’s think of a real-world game which might have this type of thing going on. Hmmm … how about: pinball, billiards, racquetball, or – one of my personal favorites – mini-golf!

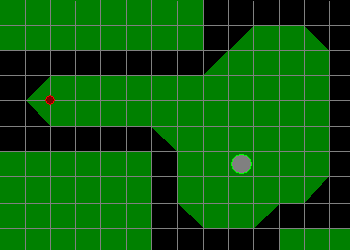
Okay, so let’s think of creating a mini-golf simulator using a basic tile engine: Each hole will be made up of a grid of either open (where the ball can freely roll) or blocked (where the ball can’t go) tiles. A basic hole could look like this:

Where the green squares are open tiles, the black squares are closed tiles, the little orange/red circle is our golf ball, and the bigger green/gray circle is the hole.

In this type of case, we’d probably want to represent our ball and the hole with a circular boundary type, and the tiles as rectangular. So, then, how do we go about determining if our ball has smacked into one of the blocker rectangles? Hey – that’s a good question! And, the basis for this tutorial …

First, I start by breaking down the different cases that can occur when mixing a circle and a rectangle. And, there are nine of them! "Nine?!" you cry, "Holy moley, guy! That’s a whole lot of ‘em!"

Well, it is and it isn’t. It "is" because we need to think about each case. And, it "isn’t" because all of the cases boil down to essentially the same test. So, here we go: the nine cases …

And those cases can be gathered into four categories:

1. Circle Inside the Rectangle (case #5 – kind of like the 5-hole on a hockey goalie J ) – this is determined when the center point of the circle is between both the top and bottom and left and right of the rectangle. This is always a collision.

2. Circle Directly Above or Below the Rectangle (cases #2 and #8) – If the circle’s center point X component is between the rectangle’s left and right, then we just need to determine which is closer – the top or bottom. Taking that side’s Y component, we subtract the circle’s Y component. If the absolute value of the result is less than the circle’s radius, we have a collision.

3. Circle Directly Left or Right of the Rectangle (cases #4 and #6) – If the circle’s center point Y component is between the rectangle’s top and bottom, then we just need to determine which side is closer – left or right. Taking that side’s X component, we subtract the circle’s X component. If the absolute value of the result is less than the circle’s radius, we have a collision (sound familiar?).

4. Circle Off a Corner of the Rectangle (cases #1, #3, #7, and #9) – If the circle is approaching the rectangle off one of its corners, then that corner point is the first thing on the rectangle that the circle can hit. So, with the nearest corner determined, find the distance between that corner and the circle’s center point. If it’s less than the circle’s radius, we have a collision.

In all of these situations, we’re basically finding the closest point on (or within) the rectangle to the circle, and we test the distance between and compare it to the circle’s radius. We can do this by setting a test point to the center of the circle, then constraining the components of that test point to those of the rectangle. The resulting point will be the point we’re looking for.

So, how about a little sample code:

First, our distance-finding function (hopefully, Almar is happy with my use of Long’s and multiplication instead of squaring J ):

Public Function FindDistance(X1 as Long, Y1 as Long, _

X2 as Long, Y2 as Long) as Double

FindDistance = Sqr((X2-X1)*(X2-X1) + (Y2-Y1)*(Y2-Y1))

End Function

 

Then, our Circle-versus-Rectangle function:

Public Function CircleRectCollision(TheCircle as udtCircle, _

TheRect as RECT) as Boolean

Dim TestX as Long, TestY as Long

TestX = TheCircle.X

TestY = TheCircle.Y

If TestX < TheRect.Left then TestX = TheRect.Left

If TestX > TheRect.Right then TestX = TheRect.Right

If TestY < TheRect.Top then TestY = TheRect.Top

If TestY > TheRect.Bottom then TestY = TheRect.Bottom

CircleRectCollision = FindDistance(TheCircle.X, _

TheCircle.Y, TestX, TextY) < TheCircle.Radius

End Function

 

This routine will find the closest point on (or within) the rectangle to the circle, then check the distance in between. If the distance is less than the circle’s radius, it will return "true" … otherwise, "false."

Sometimes, we don’t want to be stuck with just a rectangular-based world – we’d like a different angle on things. For example, we might want to soften the corners a bit by adding some 45-degree angle transitions. In our mini-golf world, it might look like this:

This will give a bit more variety and make things seem a little more organic. However, this will change how we represent our tiles and how we go about detecting collisions.

Within our tile-based world, these triangles are really just rectangles that are missing a corner. So, inside of our user-defined type used to represent our tiles, not only would we have a RECT to describe our bounding rectangle, but also we’ll need another variable to indicate what type of rectangle/triangle we’re dealing with.

Sounds like a good use of an enumeration type:

Public Enum enumTriangleType

Rectangle = 0

UpperLeft = 1

UpperRight = 2

LowerLeft = 3

LowerRight = 4

End Enum

Except for the first item in the list (Rectangle), each value in the Enum will indicate which corner is "missing" from the rectangle to form the triangle.

But, each type of triangle will need slightly different tests done to determine collisions. So we’ll need to create a select/case structure in our circle-versus-triangle detection routine. The shell of the routine could be something like this:

Public Function CircleTileCollision(TheCircle as udtCircle, _

TileRect as RECT, TileType as enumTriangleType) _

as Boolean

Select Case TileType

Case Rectangle

CircleTileCollision = _

CircleRectCollision(TheCircle, TileRect)

Case UpperLeft

‘Do UpperLeft-focused Tests Here

Case UpperRight

‘Do UpperRight-focused Tests Here

Case LowerLeft

‘Do LowerLeft-focused Tests Here

Case LowerRight

‘Do LowerRight-focused Tests Here

Case Else

CircleTileCollision = False

End Select

End Function

To work through the different test cases involved with a triangle, I’m just going to focus on one of the four types – LowerLeft. With this type of triangle, there are seven different collision cases:

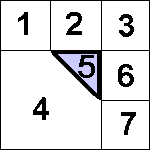
As you can see, there are some cases that can be treated the same way as we did with a rectangle. Namely, those that approach one of the square faces (#2 – top and #6 – right), and those that approach one of the corners (#1, #3, and #7). We could cover those in code by writing:

If TheCircle.X > TileRect.Right or TheCircle.Y _

< TileRect.Top then

CircleTileCollision = CircleRectCollision(TheCircle, _

TileRect)

End If

Otherwise, only cases #4 (approaching the angled face) and #5 (circle inside the triangle) present new problems.

First, let’s explore case #5 – circle inside the triangle. Since our triangle is nicely made up of a rectangle, we know that it is a right triangle, and that two of the sides are square to our grid (meaning one vertical face and one horizontal face). So, if we’ve already check for cases #1, #2, #3, #6, and #7, then we know that the center of the circle has to be left of TileRect.Right and below TileRect.Top.

We can quickly throw-out this idea if either the circle’s X is less than TileRect.Left or the circle’s Y is greater than TileRect.Bottom. If either is true, then we know that this can’t be a case #5, and we should move on to the next section, and check for case #4.

However, if it is within the rectangle, then we just need to check if it’s to the upper-right of the angled line. (Of course, with the other 3 types of triangles we’ll need to alter the side of the angled line that we check for.)

We know that the angled line runs from the TopLeft of the RECT to the BottomRight. This means that when its Y is the same as TileRect.Top, its X is the same as TileRect.Left. And when its Y is the same as TileRect.Bottom, its X is the same as TileRect.Right. So, we can calculate slopes for both components, as follows:

Then we check if the X is where it should be, based upon where the Y is, and if the Y is where it should be, based upon where the X is … what?! Based upon the slopes that we just calculated, we can determine if the X is further to the right than the line and if the Y is above the line. Like so:

The above code will work with any rectangles, including non-squares. If our rectangles are all squares, this simplifies things quite a bit. If you think through it, it will mean that both SlopeForX and SlopeForY will be equal to 1. This means that Xcheck and Ycheck are essentially checking the same thing. So, for square tiles, we can skip the slope calculations and the double-checking and just do this:

That leaves us with figuring out if our circle has collided with the angled line (from the outside), otherwise known (within this tutorial anyway) as case #4.

This test is going to use up more time than any of the other tests, so we should see if there’s a way to quickly eliminate the circle as being too far away from the line. Imagine the circle being exactly its radius’ distance from the line, perpendicular to one of the ends of the angled line. In fact, you don’t even have to imagine it … I’ll draw it for you:

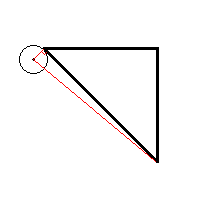
You’ll notice that the red triangle is a right triangle, and the long hypotenuse can be calculated from the length of the line and the radius of the circle.

LineLength = FindDistance(TileRect.Left, TileRect.Top, _

TileRect.Right, TileRect.Bottom)

Hyp = Sqr((TheCircle.Radius * TheCircle.Radius) + _

(LineLength * LineLength))

This is the furthest away that the circle can be from one end of the line, while being perpendicular to the other end. Therefore, the circle cannot be that distance away from both points at the same time. So, we have our quick check:

If FindDistance(TheCircle.X, TheCircle.Y, TileRect.Left, _

TileRect.Top) > Hyp and _

FindDistance(TheCircle.X, TheCircle.Y, _

TileRect.Right, TileRect.Bottom) > Hyp then

CircleTileCollision = False

Exit Sub

End If

One quick note on speeding things up with this: Since we know the tiles we’re dealing with ahead of time, we could pre-calculate the length of the angled line and store it within the tile definition. Then, we won’t have to do the LineLength calculation each cycle. And, if all of the possible angled lines are the same length (which will be the case when using consistently-sized, square tiles), then that value can be stored as a constant. And, since we’ll probably know the circle radius ahead of time, we could pre-calculate the "Hyp" value between the circle and the standard line length and store that within the sprite’s definition – that would be the fastest yet.

So, if we’ve made it past all of those other tests, then we know that our circle is approaching the triangle from outside its angled line, and that it’s close enough to test if it’s touching.

The process, in words, goes as follows:

1. Starting at the close end of the angled line, move down the slope of the line toward the other end

2. At each point along the way, check the distance from that point to the center of the circle

a. If the distance is less than the circle’s radius, then a collision has been detected

b. If the distance is more than from the previous point, a collision can no longer occur; indicate so, and exit the sub

In code we’d do something like:

This makes for a potentially long and ugly loop of if/then’s and logical tests, but for the most part, they should still run pretty quickly.

So, where does this leave us? Well, now we know how to detect collisions between objects with different bounding types – namely, circles versus rectangles and rectangle-based-triangles. So what happens after the collision?

First, we probably want to do some interpolative nearing … um, what? We’ll want to take our object back in time to the exact instant before the collision – this will give us a near-enough approximation to continue from.

Next, we’ll want some type of physics-based reaction to the situation. What happens when one of our mini-golf balls hits another ball … what about when it gets banked off one of those lovely wooden sidewalls?

As we’ll find, doing the physics for a circular object bouncing off the squared-off sides of a rectangle is quite easy. In fact, if our triangle uses a 45-degree angle, it’s still not very difficult. But, what about non-45-degree angled walls, and what about ball-versus-ball contact?

That, my friends, is what Part 2 of this pair of tutorials is for! Until then …